StatLit banner

Standardizing

Milo Schield, Editor

Jerome Cornfield

Standardization or Standardizing:

Standardization is a simple statistical technique for taking into account (controlling for) the influence of a binary confounder without multivariate regression. See:

For an application of standardization, see Confound Those Speculative Statistics by Schield, 2009 ASA.
To see how standardizing can influence statistical significance, see Schield 2013 ASA.
For more on confounding, see Definitions of Confounding.

Confounding (Simpson's Paradox) is central to statistical literacy.

Confounding and “controlling for” are to statistical literacy

  • as context and alternate explanations are to critical thinking.
  • as randomness and statistical significance are to statistical inference.

Confounding is one way of describing an interaction: an association involving at least three related factors.

Association involving counts are contextual. Even if the number unemployed is bigger in California than in Iowa, the unemployment rate can be smaller in California than in Iowa.

Associations involving ratios (averages, rates and percentages) are contextual. See the example below.

While there is no test for confounding, Jerome Cornfield (pictured above) showed that an association could not be nullified or reversed unless the associations with confounder was at least as strong as the observed association between predictor and outcome. See Simpson's Paradox and  Cornfield's Condition by Schield (1999).

Simpson's Paradox is an extreme case of standardization—where an association between two factors reverses after taking into account the influence of a third factor.

  • Simpson's paradox is found in observational data—data common in business, education and public policy.
  • Simpson's Paradox is the “Achilles heel” in inferring causation in the social sciences.
  • Terwilliger and Schield (2004) found that 10% of the statistically-significant differences in NAEP scores are spurious.
  • The smaller the effect size, the greater the opportunity for confounding.
  • Effect size and confounder resistance are as important to statistical literacy as sample size and statistical significance are to statistical inference. 

Yet, very few statistics textbooks spend much time on confounding, Simpson's Paradox or standardizing.

The following show (1) what Simpson's Paradox is, (2) how it works dynamically and (3) some articles on Simpson's Paradox.

Simpson's Paradox: An Example

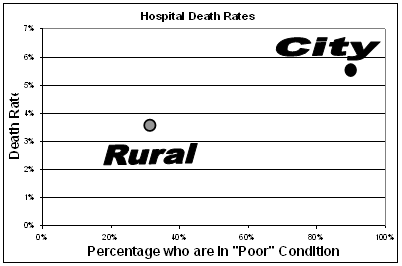
Consider the percentage of patients who die at two hospitals: City and Rural. As shown in the graph on the left, the patient death rate is higher at City (5.5%) than at Rural (3.0%). While one might infer that Rural is the better hospital, association does not prove causation. An alternate explanation is the difference in mixture of patients in poor condition. At City, 90% are in poor condition while at the Rural hospital only 30% are in poor condition.

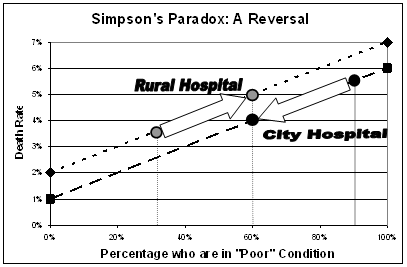
The graph on the right clearly shows that patients in poor condition have a higher death rate than other patients.

Among patients in poor condition (on the right side), the death rate is 7% at the Rural hospital and 6% at the City hospital. Among patients not in poor condition (on the left side), the death rate is 2% at the Rural hospital and 1% at the City hospital. The diagonal lines are the weighted average lines. The average reflects the mixture of the two groups. The 5.5% average death rate at city hospital reflects the fact that 90% of the city patients are in poor condition. The 3.5% average death rate at rural hospital reflects the fact that only 30% of the rural hospital patients are in poor condition.

Hospital Death Rates Simpson's Paradox: A Reversal

What would the death rates be if both hospitals had the same mix of patients?

We need to standardize: to recalculate the death rates using the same mix of patients.

Suppose that for both hospitals combined, 60% of all patients were in poor condition. Suppose we gave each hospital this same mix.

Note that we are not changing the death rates for any subgroup—we are just changing the mixture of the subgroups.

In that case, the average death rate at the City hospital would decrease while the average death rate at the rural hospital would increase.

And in this particular case, they reversed. The standardized death rate is higher for Rural than for City.

This reversal is Simpson's Paradox. The difference in mix is confounded (tangled up) with the difference in death rates for the two hospitals. Standardizing is one way to untangle the influence of a binary confounder.

Standardizing Interactively On-Line

On-line interactive versions of this standardizing technique are available.

Changing the data changes the standardized values in the graph.

General Articles on Simpson's Paradox:

Simpson's Paradox and Cornfield's Conditions (1999)
by Milo Schield, Augsburg College, Director of the W. M. Keck Statistical Literacy Project

Abstract: Simpson's Paradox occurs when an observed association is spurious—reversed after taking into account a confounding factor. At best, Simpson's Paradox is used to argue that association is not causation. At worst, Simpson's Paradox is used to argue that induction is impossible in observational studies (that all arguments from association to causation are equally suspect) since any association could possibly be reversed by some yet unknown confounding factor. This paper reviews Cornfield's conditions—the necessary conditions for Simpson's Paradox—and argues that a simple-difference form of these conditions can be used to establish a minimum effect size for any potential confounder. Cornfield's minimum effect size is asserted to be a key element in statistical literacy. In order to teach this important concept, a graphical technique was developed to illustrate percentage-point difference comparisons. Some preliminary results of teaching these ideas in an introductory statistics course are presented.

Three Graphs to Promote Statistical Literacy (2004)
by Milo Schield, Augsburg College, Director of the W. M. Keck Statistical Literacy Project

Abstract: Graphical techniques have been used in introductory statistics to teach three big statistical topics: (1) confounding (which can result in Simpson’s Paradox), (2) statistical significance and (3) the vulnerability of statistical significance to confounding. These graphical techniques have been used to teach students as part of the W. M. Keck Statistical Literacy project. These graphs have transformed statistical education at Augsburg College; they can change statistical education everywhere.

Real-World Examples of Simpson's Paradox:

Instance of Simpson's Paradox in NAEP Data  (thanks to David Stein and Bob Hayden) [Broken link 12/08]

Frequency of Simpson's Paradox in NAEP Data (4/2004)
by James Terwilliger (NAEP Coordinator, Minnesota Department of Education)
and Milo Schield, Augsburg College, Director of the W. M. Keck Statistical Literacy Project

Abstract (extract): In state education data, Simpson’s Paradox occurs for two states when their difference in scores has the opposite sign of the score differences for each of the state subgroups. Simpson’s Paradox is a specific manifestation of statistical confounding. The paradox has been understood for many years but is usually regarded as simply a curious anomaly.

The purpose of this paper is to show that Simpson’s Paradox is not rare in NAEP data. NAEP public-school data are analyzed for 2000n Grade 4 Math and 2002 Grade 8 Reading. Approximately 100 instances of Simpson’s Paradox are found per data set based on the influence of three confounders: family income, school location and race/ethnicity.

As a percentage of all pairs of state differences in the same data that are statistically significant, 4% are reversed using a conservative approach while 10% are reversed using a more liberal approach. All Simpson’s reversals—whether statistically significant or not—are argued to have “journalistic significance” because of their political significance. The failure to allow adjustments for confounders can lead to a serious misinterpretation of the results which in turn can lead to questionable policies.

Links involving Simpson's Paradox:

Articles Involving the Cornfield Conditions:

  • Wikipedia: Simpson's Paradox
  • Ding, P., & Vanderweele, T. (2014). Generalized cornfield conditions for the risk difference. Biometrika, 101, 1–13.
  • Ding, P., & Vanderweele, T. (2016). Sensitivity analysis without assumptions. Epidemiology, 27, 368–377.
  • Ding, P., & VanderWeele, T. (2017). Sensitivity analysis in observational research: Introducing the E-value. Annals of Internal Medicine, 167(4), 268–274.

Examples of Simpson's Paradox

Articles involving Simpson's Paradox:

  • Blyth, CR (1972) On Simpson's Paradox and the Sure-Thing Principle. 1972 Journal of the American Statistical Association 67(338):364-366. DOI10.2307/2284382
  • Samuels, Myra L. (1993). Simpson's Paradox and Related Phenomena. Journal of the American Statistical Association Volume 88, 1993 - Issue 421 Published online: 20 Dec 2012
  • Pearl, Judea (2014). Comment: Understanding Simpson’s Paradox. Pages 8-13 Published online: 21 Feb 2014